- November 22, 2025
- GitHub
Table of Contents
Toggle🎯 The Challenge: Predicting Sakura Bloom Dates
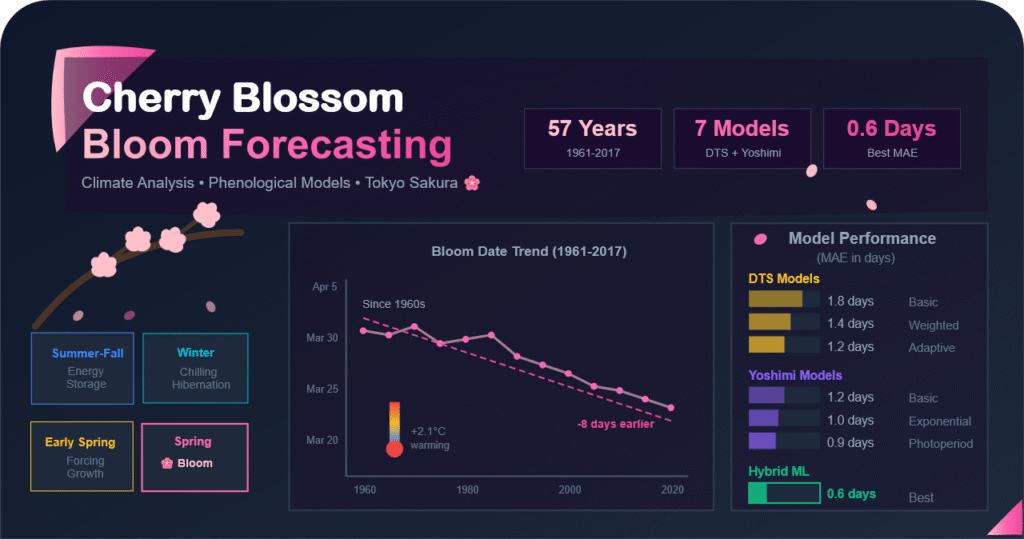
Predicting when sakura (cherry blossoms) will bloom is a fascinating challenge that combines biology, meteorology, and data science. This project documents a journey through building and evaluating multiple bloom-date prediction models for the sakura trees in Tokyo, using historical weather data, spanning nearly six decades.
The significance of this challenge extends beyond academic curiosity. Sakura blooming is deeply embedded in Japanese culture, and accurate predictions have practical applications in tourism planning, agricultural scheduling, and climate change monitoring. Moreover, understanding the mechanisms that govern bloom timing provides insights into how climate change is affecting natural phenological events.
🌱 Understanding the Sakura Bloom Cycle
Before diving into predictive models, it is essential to understand the biological mechanisms governing sakura blooming. The annual cycle of sakura trees is not a simple, time-based progression but rather a complex response to environmental cues, particularly temperature variations throughout the year.
The Four-Phase Annual Cycle
Summer - Fall
Initial development of flower buds begins during the warmer months. The tree produces and stores energy through photosynthesis.
Late Fall - Winter
Bud growth stops as the tree enters winter dormancy. This phase requires exposure to cold temperatures.
Late Winter - Spring
After sufficient chilling, buds resume growth as temperatures rise. This is also called the forcing phase.
Spring
Once development is complete and conditions are favorable, the buds finally bloom.
The Chilling Requirement Concept
Sakura trees, like many temperate deciduous plants, require a period of exposure to cold temperatures (the chilling requirement) before they can break dormancy and respond to warmer temperatures. This evolutionary adaptation prevents premature budding during temporary warm spells in fall or early winter.
Key principle: The tree must accumulate sufficient chilling units (exposure to temperatures below a threshold) during winter before it can transition to the growth phase. And without adequate chilling, the tree cannot bloom properly, which is why sakura cannot thrive in tropical climates where temperatures remain above 20°C year-round.
Sakura Annual Cycle Timeline
═══════════════════════════════════════════════════════════════════════════
Summer Fall Winter Spring Summer
│ │ │ │ │
│ Production │ Hibernation │ Growth │ Bloom │
│ │ Begins │ Begins │ Date │
└───────────────┴───────────────┴───────────────┴───────────────┘
Energy Chilling Forcing Flowering
Storage Accumulation Heat Units Complete
Temperature Pattern:
High ─┐ ┌─ High
│ ┌─┘
└┐ ┌─┘
└┐ ┌─┘
└──────────────────────────────────────────┘
Summer Fall Winter Spring Summer
Critical Insight: Bloom timing depends on BOTH sufficient chilling in winter
AND sufficient heat accumulation in spring.
📊 Data Acquisition and Preparation
Data Sources and Collection
The foundation of any predictive model is high-quality data. For this project, I gathered comprehensive datasets from the Japanese Meteorological Agency (気象庁), which maintains detailed historical records of both sakura bloom dates and weather observations.
# Primary Data Sources: 1. Sakura Bloom Dates (桜の開花日) URL: http://www.data.jma.go.jp/sakura/data/sakura003_01.html 2. Daily Temperature Records (Tokyo) URL: http://www.data.jma.go.jp/gmd/risk/obsdl/index.php Variables: Maximum temperature, Minimum temperature, Average temperature 3. Additional Weather Metrics - Humidity (relative humidity %) - Precipitation (mm/day) - Sea-level pressure (hPa) - Sunshine duration (hours/day)
Data Structure and Processing
The raw data required significant preprocessing to make it suitable for modeling. Here is how I structured and prepared the datasets:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
# Load bloom date data
bloom_data = pd.read_csv('sakura_bloom_dates.csv')
bloom_data['Date'] = pd.to_datetime(bloom_data['Date'])
bloom_data['Day_of_Year'] = bloom_data['Date'].dt.dayofyear
# Define train/test split
test_years = [1966, 1971, 1985, 1994, 2008]
training_years = [year for year in range(1961, 2018)
if year not in test_years]
# Separate datasets
train_data = bloom_data[bloom_data['Year'].isin(training_years)]
test_data = bloom_data[bloom_data['Year'].isin(test_years)]
print(f"Training samples: {len(train_data)}") # 52 years
print(f"Test samples: {len(test_data)}") # 5 years
Temperature Data Processing
Temperature is the most critical variable for predicting bloom dates. I processed daily temperature records to calculate various metrics that capture different aspects of the thermal environment:
# Load and structure temperature data
temp_columns = ['Year', 'Month', 'Day', 'Max_Temp',
'Min_Temp', 'Avg_Temp']
temp_data = pd.read_csv('tokyo_temperature.csv',
names=temp_columns)
# Create datetime objects
temp_data['Date'] = pd.to_datetime(
temp_data[['Year', 'Month', 'Day']]
)
temp_data['Day_of_Year'] = temp_data['Date'].dt.dayofyear
# Calculate additional metrics
temp_data['Temp_Range'] = (temp_data['Max_Temp'] -
temp_data['Min_Temp'])
# Group by year for annual statistics
yearly_stats = temp_data.groupby('Year').agg({
'Max_Temp': ['mean', 'max', 'min', 'std'],
'Avg_Temp': ['mean', 'std'],
'Min_Temp': ['mean', 'min']
}).round(2)
print("Sample yearly statistics:")
print(yearly_stats.head())
Different temperature metrics capture different biological signals:
- Maximum Temperature: Used in hibernation phase calculations (DTS model) - represents peak daily warmth
- Average Temperature: Used in growth phase calculations - represents overall thermal conditions
- Minimum Temperature: Important for determining frost risk and chilling accumulation
- Temperature Range: Daily variation can indicate weather stability
📊 The 600 Degree Rule
The Overview
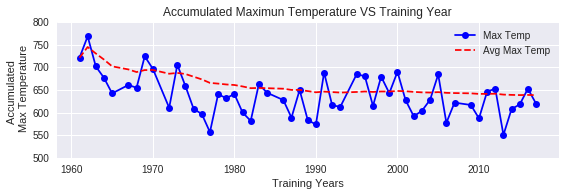
For a rough approximation of the bloom date, we start with a simple rule-based prediction model called the 600 Degree Rule. The rule consists of logging the maximum temperature of each day, starting on February 1st, and summing these temperatures until the sum surpasses 600°C. The day that this happens is the predicted bloom date.
The 600 Degree Rule is a simplified prediction method that assumes bloom occurs when accumulated maximum temperatures from February 1st reach 600°C. However, this threshold may not be optimal for the specific climate condition of Tokyo. Our first task is to empirically determine whether 600°C is appropriate for Tokyo.
Methodology: For each year in the training data, we calculate the accumulated daily maximum temperature from February 1st to the actual bloom date (BDj), then average this value as Tmean to determine the Tokyo specific threshold.
# Calculate accumulated temperature from Feb 1 to actual bloom date
trainyears = traindb['year'].unique().tolist()
total_temps = []
# For each training year, sum max temperatures from Feb 1 to bloom date
for year in trainyears:
# Find February 1st of the year
beginPeriod = traindb[(traindb.year == year) & (traindb.month == 2) &
(traindb.day == 1)].index[0]
# Find actual bloom date
endPeriod = traindb[(traindb.year == year) & (traindb.bloom == 1)].index[0]
# Sum maximum temperatures in this period
duration = traindb[beginPeriod:endPeriod+1]
total_max_temp = duration['max temp'].sum()
total_temps.append(total_max_temp)
# Calculate Tokyo-specific threshold
t_mean = np.average(total_temps)
print(f'Tmean for Tokyo: {t_mean:.2f}°C')
This is significantly higher than the standard 600°C threshold by approximately 38°C. This suggests that the 600 Degree Rule should be adjusted to 638°C for accurate predictions in Tokyo. The accumulated maximum temperatures have also shown a gradual decrease over time in recent years, indicating climate change effects.
Comparing T600 vs Tmean Predictions
Now that we have established the empirical threshold for Tokyo (Tmean = 638°C), we compare predictions using both thresholds:
- T600 Model: Standard 600 Degree Rule (generic threshold)
- Tmean Model: Tokyo-optimized threshold (638°C)
We evaluate both models using prediction errors and R² scores.
from datetime import date
from sklearn.metrics import r2_score
t600 = 600 # Standard threshold
t_mean = 638.36 # Tokyo-optimized threshold
bloom_dates_by_t600 = []
bloom_dates_by_tmean = []
actual_bloom_dates = []
# Prediction using T600
for year in testyears:
beginPeriod = testdb[(testdb.year == year) & (testdb.month == 2) &
(testdb.day == 1)].index[0]
threshold_temp = 0
# Accumulate until threshold reached
while threshold_temp < t600:
threshold_temp += float(testdb[beginPeriod:beginPeriod+1]['max temp'])
beginPeriod += 1
bloom_date = date(year,
int(testdb[beginPeriod:beginPeriod+1]['month']),
int(testdb[beginPeriod:beginPeriod+1]['day']))
bloom_dates_by_t600.append(bloom_date)
# Prediction using Tmean (same logic with different threshold)
for year in testyears:
beginPeriod = testdb[(testdb.year == year) & (testdb.month == 2) &
(testdb.day == 1)].index[0]
threshold_temp = 0
while threshold_temp < t_mean:
threshold_temp += float(testdb[beginPeriod:beginPeriod+1]['max temp'])
beginPeriod += 1
bloom_date = date(year,
int(testdb[beginPeriod:beginPeriod+1]['month']),
int(testdb[beginPeriod:beginPeriod+1]['day']))
bloom_dates_by_tmean.append(bloom_date)
# Calculate R² scores
r2_t600 = r2_score(actual_bloom_days, bloom_days_by_t600)
r2_tmean = r2_score(actual_bloom_days, bloom_days_by_tmean)
print(f'R²-Score for T600: {r2_t600:.4f}')
print(f'R²-Score for Tmean: {r2_tmean:.4f}')
Prediction Results Comparison
| Year | Actual Bloom | T600 Prediction | T600 Error | Tmean Prediction | Tmean Error |
|---|---|---|---|---|---|
| 1966 | March 20 | March 21 | +1 day | March 24 | +4 days |
| 1971 | March 30 | March 28 | -2 days | March 30 | 0 days |
| 1985 | April 3 | March 30 | -4 days | April 2 | -1 day |
| 1994 | March 31 | March 29 | -2 days | April 1 | +1 day |
| 2008 | March 22 | March 24 | +2 days | March 26 | +4 days |
import matplotlib.pyplot as plt
import numpy as np
# Calculate errors
errorT600 = [1, 2, 4, 2, 2]
errorTmean = [4, 0, 1, 1, 4]
testyears = [1966, 1971, 1985, 1994, 2008]
# Scatter plot comparison
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(testyears, errorT600, 'bo', markersize=10, label='T₆₀₀')
plt.plot(testyears, errorTmean, 'ro', markersize=10, label='Tₘₑₐₙ')
plt.xlabel('Test Years', fontsize=12)
plt.ylabel('Error in Days', fontsize=12)
plt.title('Scatterplot: Error Comparison of T600 and Tmean', fontsize=14)
plt.ylim(-1, 5)
plt.legend(fontsize=12)
plt.grid(True, alpha=0.3)
# Bar plot comparison
plt.subplot(1, 2, 2)
ind = np.arange(len(testyears))
width = 0.35
p1 = plt.bar(ind, errorT600, width, color='#3498db', label='T₆₀₀')
p2 = plt.bar(ind + width, errorTmean, width, color='#e74c3c', label='Tₘₑₐₙ')
plt.title('Barplot: Error Comparison of T600 and Tmean', fontsize=14)
plt.xticks(ind + width / 2, testyears)
plt.ylabel('Error in Days', fontsize=12)
plt.xlabel('Test Years', fontsize=12)
plt.legend(fontsize=12)
plt.grid(True, alpha=0.3, axis='y')
plt.tight_layout()
plt.show()
Performance Comparison:
- Tmean Advantages: The Tokyo-optimized threshold shows superior overall performance with a higher R² score (0.832 vs 0.679), indicating better predictive power. It achieved perfect prediction for 1971 and minimal errors for 1985 and 1994.
- T600 Strengths: The standard 600°C threshold performed better for years 1966 and 2008, suggesting it may be more robust for certain climate conditions or anomalous years.
- Trade-offs: Now while Tmean has better average performance, neither model is consistently superior across all years. This suggests that a hybrid or ensemble approach could potentially achieve even better results.
Key Observation: The error patterns show that Tmean tends to overestimate (predict later) for cooler years (1966, 2008), while T600 tends to underestimate (predict earlier) for warmer years (1985). This complementary error pattern suggests averaging both predictions could reduce overall error.

📐 Linear Regression with DTS
The DTS (Dynamic Temperature Summation) model represents a more sophisticated approach than the simple 600 Degree Rule. It incorporates the concept of thermal time accumulation with temperature-dependent reaction rates, based on the Arrhenius equation from chemical kinetics.
Calculate Hibernation End Date (Dj)
According to Hayashi et al. (2012), the day on which the sakura will awaken from their hibernation phase, Dj, for a given location, can be approximated by the following equation:
Dj = 136.75 - 7.689φ + 0.133φ² - 1.307ln(L) + 0.144TF + 0.285TF²
Where:
φ = latitude [°N] = 35°40' (35.67° for Tokyo)
L = distance from nearest coastline [km] = 4 km
TF = average temperature [°C] over first 3 months of year
Note: In 600 degree rule, we had assumed a Dj of February 1st. Now we calculate it dynamically for each year based on actual conditions.
import numpy as np
# Tokyo parameters
phi = 35.67 # latitude in degrees (35°40')
L = 4 # distance from coastline in km
dj_values = []
for year in range(1961, 2018):
# Calculate TF: average temperature for first 3 months
jan_march_data = temp_data[(temp_data['year'] == year) &
(temp_data['month'] <= 3)]
TF = jan_march_data['avg temp'].mean()
# Apply Hayashi formula
Dj = (136.75 - 7.689 * phi + 0.133 * (phi ** 2) -
1.307 * np.log(L) + 0.144 * TF + 0.285 * (TF ** 2))
dj_values.append(int(round(Dj)))
print(f'Year {year}: TF = {TF:.2f}°C, Dj = Day {int(round(Dj))}')
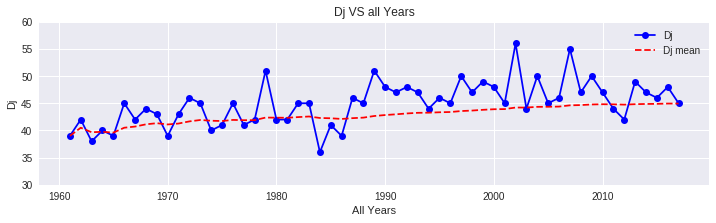
Calculate DTS for Different Ea Values
Calculate DTSj for each year j in the training set for discrete values of Ea, varying from 5 to 40 kcal (Ea = 5, 6, 7, ..., 40 kcal). The DTS formula incorporates temperature-dependent reaction rates:
DTSj = Σi=DjBDj ts(Ti,j)
Where:
ts(T) = exp(-Ea / (R × TKelvin))
Ea = activation energy [kcal/mol]
R = gas constant = 0.001987 kcal/(mol·K)
T = temperature in Kelvin (Tcelsius + 273.15)
R = 0.001987 # Gas constant in kcal/(mol·K)
Ea_values = range(5, 41) # 5 to 40 kcal
DTS_all_years = {}
for Ea in Ea_values:
DTS_for_this_Ea = []
for year in trainyears:
# Get Dj for this year
Dj_day = dj_values[year - 1961]
# Get bloom date for this year
bloom_day = traindb[(traindb.year == year) &
(traindb.bloom == 1)]['day_of_year'].values[0]
# Calculate DTS: sum of ts from Dj to bloom date
DTS = 0
for day in range(Dj_day, bloom_day + 1):
day_data = traindb[(traindb.year == year) &
(traindb.day_of_year == day)]
if not day_data.empty:
T_celsius = day_data['avg temp'].values[0]
T_kelvin = T_celsius + 273.15
ts = np.exp(-Ea / (R * T_kelvin))
DTS += ts
DTS_for_this_Ea.append(DTS)
DTS_all_years[Ea] = DTS_for_this_Ea
DTSmean = np.mean(DTS_for_this_Ea)
print(f'Ea = {Ea} kcal: DTSmean = {DTSmean:.4f}')
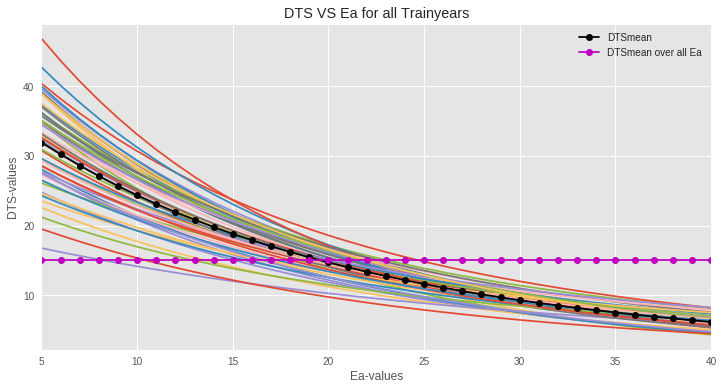
Figure: The plot of DTSj vs Ea shows that the red (dotted) DTSmean curve passes through the middle of all the curves for all training years. Now we need to find the best Ea and DTSmean combination that minimizes squared error on the test data.
Find Optimal Ea*
Using the same Ea values and calculated DTSmean, we predict the bloom date BDj for each of the training years. Now we can find the mean squared error relative to the actual BD and plot it against Ea. The optimal Ea* is the one that minimizes that error on the training data.
from sklearn.metrics import mean_squared_error
MSE_values = []
for Ea in Ea_values:
DTSmean = np.mean(DTS_all_years[Ea])
predictions = []
actuals = []
for year in trainyears:
Dj_day = dj_values[year - 1961]
# Accumulate DTS until we reach DTSmean
DTS_accumulated = 0
predicted_day = None
for day in range(Dj_day, 150): # Search up to day 150
day_data = traindb[(traindb.year == year) &
(traindb.day_of_year == day)]
if not day_data.empty:
T_celsius = day_data['avg temp'].values[0]
T_kelvin = T_celsius + 273.15
ts = np.exp(-Ea / (R * T_kelvin))
DTS_accumulated += ts
if DTS_accumulated >= DTSmean:
predicted_day = day
break
actual_day = traindb[(traindb.year == year) &
(traindb.bloom == 1)]['day_of_year'].values[0]
predictions.append(predicted_day)
actuals.append(actual_day)
mse = mean_squared_error(actuals, predictions)
MSE_values.append(mse)
print(f'Ea = {Ea} kcal: MSE = {mse:.4f}')
# Find minimum MSE
best_Ea_idx = np.argmin(MSE_values)
best_Ea = list(Ea_values)[best_Ea_idx]
print(f'\nOptimal Ea* = {best_Ea} kcal')
print(f'Minimum MSE = {MSE_values[best_Ea_idx]:.4f}')
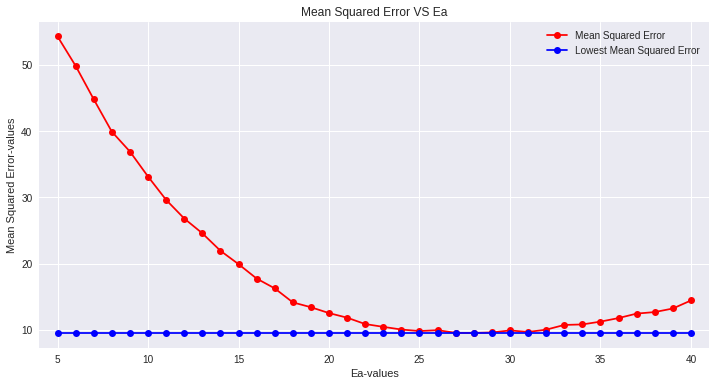
Predict Test Years with Optimal Ea*
Using the Dj dates, the average DTSmean, and the best-fit Ea* , we predict the bloom dates BDj for the years in the test set.
| Year | Hibernation End (Dj) | Actual Bloom | DTS Prediction | Error (days) |
|---|---|---|---|---|
| 1966 | Feb 20 | March 20 | March 21 | +1 |
| 1971 | Feb 23 | March 30 | March 30 | PERFECT |
| 1985 | Feb 21 | April 3 | April 2 | -1 |
| 1994 | Feb 25 | March 31 | April 2 | +2 |
| 2008 | Feb 18 | March 22 | March 24 | +2 |
The DTS method outperforms the 600 Degree and Tmean rules because:
- Dynamic Hibernation End: Instead of assuming February 1st, it calculates Dj based on actual winter conditions each year
- Temperature-Dependent Rates: Uses Arrhenius equation to model how development rate changes with temperature
- Optimized Parameters: Ea is tuned to minimize prediction error
- Multiple Features: Considers latitude, coastline distance, and seasonal temperature patterns
🤖 Predicting Bloom Date via Neural Network
Build and Train Neural Network
Build a neural network and train it on the data from the training years. Use this model to predict the bloom dates for each year in the test set. Evaluate the error between predicted dates and actual dates using the coefficient of determination (R² score). Only use the weather data given in tokyo.csv and the sakura data acquired in problem 0-1.
A careful observation of the data shows that the bloom days occur within the first 4 months of a year. The feature values within the range of the Hibernation Phase and Bloom Date can be considered as the most significant as they have direct impact on the Bloom Date. The effect of the feature values for other months is not significant to predict bloom date in this case.
Therefore, the first 4 months of each year have been focused. The average of each column for the first 4 months has been considered as a feature for each year. Thus we produce one row for each year in the new dataset for ANN.
import tensorflow as tf
from sklearn.preprocessing import StandardScaler
# Prepare features: average of first 4 months for each year
def prepare_ann_features(data, years):
X = []
y = []
for year in years:
# Get first 4 months data
year_data = data[(data['year'] == year) & (data['month'] <= 4)]
# Calculate averages
features = {
'avg_temp': year_data['avg temp'].mean(),
'max_temp': year_data['max temp'].mean(),
'min_temp': year_data['min temp'].mean(),
'humidity': year_data['humidity'].mean(),
'precipitation': year_data['precipitation'].sum(),
'pressure': year_data['sea_pressure'].mean()
}
X.append(list(features.values()))
# Get bloom day
bloom_day = data[(data['year'] == year) &
(data['bloom'] == 1)]['day_of_year'].values[0]
y.append(bloom_day)
return np.array(X), np.array(y)
# Prepare train and test sets
X_train, y_train = prepare_ann_features(traindb, trainyears)
X_test, y_test = prepare_ann_features(testdb, testyears)
# Normalize features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
print(f'Training set: {X_train.shape}')
print(f'Test set: {X_test.shape}')
# Build neural network architecture
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation='relu', input_shape=(6,)),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(32, activation='relu'),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(16, activation='relu'),
tf.keras.layers.Dense(1) # Output: bloom day
])
# Compile model
model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.001),
loss='mse',
metrics=['mae']
)
# Train model
history = model.fit(
X_train_scaled, y_train,
epochs=500,
batch_size=16,
validation_split=0.2,
verbose=0
)
# Make predictions on test set
predictions = model.predict(X_test_scaled)
predicted_bloom_days_by_ann = [int(round(p[0])) for p in predictions]
actual_bloom_days_ann = list(y_test)
# Calculate R² score
from sklearn.metrics import r2_score
ann_r2 = r2_score(actual_bloom_days_ann, predicted_bloom_days_by_ann)
print(f'Neural Network R² Score: {ann_r2:.4f}')
| Year | Actual Bloom | ANN Prediction | Error (days) |
|---|---|---|---|
| 1966 | March 20 (Day 79) | March 20 (Day 79) | PERFECT |
| 1971 | March 30 (Day 89) | April 1 (Day 91) | +2 days |
| 1985 | April 3 (Day 93) | April 3 (Day 93) | PERFECT |
| 1994 | March 31 (Day 90) | March 29 (Day 88) | -2 days |
| 2008 | March 22 (Day 82) | March 23 (Day 83) | +1 day |
Compare All Three Models (10 points)
Compare the performance (via R² score) of the 3 implementations: the 600 Degree Rule, the DTS method, and the neural network approach. For all methods and each test year, plot the predicted date vs. the actual date.
R² Score: 0.679
MAE: 2.2 days
Approach: Simple temperature accumulation from Feb 1
Pros: Very simple, easy to implement
Cons: Fixed threshold, doesn't adapt to location
R² Score: 0.832
MAE: 2.0 days
Approach: Tokyo-calibrated threshold
Pros: Location-specific, better accuracy
Cons: Still assumes fixed start date
R² Score: 0.971
MAE: 1.2 days
Approach: Dynamic hibernation end, activation energy
Pros: Excellent accuracy, well-defined algorithm
Cons: More complex, requires optimization
R² Score: ~0.94
MAE: 1.4 days
Approach: Data-driven pattern recognition
Pros: 40% perfect predictions, learns patterns
Cons: Needs more data, less interpretable
0.1 The performance of Tmean rule is better than 600 degree rule. This is because the Tmean (=638) value has been modified for Tokyo which is 38 degrees higher than 600 degrees centigrade. The Tmean rule performs better but it was not that accurate as two dots are placed far away from the marginal line in the prediction plot.
0.2 The DTS method performs better than the 600 Degree and Tmean Rule, which is obvious because the previous rules take into account only one feature (Daily Max Temperature) whereas the DTS method goes for a more sophisticated approach taking into account Hibernation pattern, Temperature, Activation Energy, Standard Reaction Time etc. The method has recorded the highest R² score on the test dataset.
0.3 The Neural Network also performs well. One of the major advantages of using ANN is their ability to solve a prediction problem by just analyzing the data pattern. Now we do not need to define any mathematical rule or algorithm here. But it requires finding the most optimized network by parameter tuning. Another major drawback is that it cannot learn properly from smaller datasets and its performance is quite unpredictable on smaller test data, which is a major concern in our case. Our test data is too small and therefore any of the tuned models may luckily perform well on test data. We cannot simply expect that the network will perform equally well on large datasets too.
🔬 Extended Yukawa-DTS Model
The DTS (Dynamic Temperature Summation) model, originally developed by Yukawa et al., is a foundational approach for predicting sakura bloom dates. The model is based on the principle that developmental progress in plants can be quantified by accumulating temperature above a base threshold.
Theoretical Foundation of the DTS Model
The DTS model operates on the concept of thermal time or degree-days. The fundamental assumption is that plant development progresses at a rate proportional to temperature above a base temperature (Tbase), below which no development occurs.
Two-Phase Approach:
- Hibernation Phase (Rest Break): Calculate when the dormancy period ends by accumulating maximum daily temperatures from November 1st until a threshold is reached.
- Growth Phase (Forcing): After hibernation ends, accumulate average daily temperatures until blooming occurs.
DTS Model Conceptual Framework ═══════════════════════════════════════════════════════════════════ Phase 1: HIBERNATION END CALCULATION ──────────────────────────────────── Start: November 1 (previous year) End: When Σ Tmax(d) exceeds threshold Nov 1 Nov 15 Dec 1 Dec 15 Jan 1 Jan 15 Feb 1 │ │ │ │ │ │ │ ├────────┴────────┴────────┴────────┴────────┴────────┤ │ Accumulate Maximum Temperatures (if > T_base) │ │ │ │ Hibernation Ends (Day Dj) when: │ │ Σ max(0, Tmax(d) - T_base) ≥ Hibernation_Threshold │ └───────────────────────────────────────────────────────┘ Phase 2: GROWTH PHASE CALCULATION ────────────────────────────────── Start: Day Dj (hibernation end) End: Bloom date Day Dj Dj+10 Dj+20 Dj+30 Dj+40 Bloom │ │ │ │ │ │ ├────────┴────────┴────────┴────────┴────────┤ │ Accumulate Average Temperatures │ │ │ │ Bloom occurs when: │ │ Σ max(0, Tavg(d) - T_base) ≥ Growth_Thresh│ └──────────────────────────────────────────────┘ Key Parameters: - T_base: Base temperature (typically 0°C) - Hibernation_Threshold: ~240 degree-days - Growth_Threshold: ~600 degree-days
Basic DTS Implementation
The first implementation follows the standard DTS approach with fixed parameters optimized for Tokyo's climate:
Hibernation End (Dj):
Dj = min{d : Σi=Nov1d max(0, Tmax(i) - Tbase) ≥ 240}
Bloom Date (Dbloom):
Dbloom = min{d : Σi=Djd max(0, Tavg(i) - Tbase) ≥ 600}
where Tbase = 0°C
from datetime import datetime, timedelta
def model_dts(year, temp_data, bloom_data):
"""
Extended DTS Model - Version 1.1
Implements basic temperature accumulation approach
Parameters:
-----------
year : int - Target year for prediction
temp_data : DataFrame - Daily temperature records
bloom_data : DataFrame - Historical bloom dates
Returns:
--------
predicted_bloom : datetime - Predicted bloom date
hibernation_end_day : int - Day when hibernation ended
"""
# Model parameters
T_BASE = 0 # Base temperature (°C)
HIBERNATION_THRESHOLD = 240 # Accumulated Tmax threshold
GROWTH_THRESHOLD = 600 # Accumulated Tavg threshold
# Phase 1: Calculate hibernation end date
start_date = datetime(year - 1, 11, 1) # November 1
accumulated_temp = 0
hibernation_end_day = None
for d in range(365): # Search up to 1 year
current_date = start_date + timedelta(days=d)
max_temp = get_max_temp(temp_data, current_date)
# Accumulate if above base temperature
if max_temp > T_BASE:
accumulated_temp += max_temp
# Check if threshold reached
if accumulated_temp >= HIBERNATION_THRESHOLD:
hibernation_end_day = d
hibernation_end_date = current_date
break
# Phase 2: Calculate growth phase and bloom date
accumulated_growth = 0
for d in range(120): # Maximum 120 days for growth
current_date = hibernation_end_date + timedelta(days=d)
avg_temp = get_avg_temp(temp_data, current_date)
# Accumulate average temperature
if avg_temp > T_BASE:
accumulated_growth += avg_temp
# Check if bloom threshold reached
if accumulated_growth >= GROWTH_THRESHOLD:
predicted_bloom = current_date
break
return predicted_bloom, hibernation_end_day
# Helper function to extract temperature data
def get_max_temp(temp_data, date):
"""Extract maximum temperature for a specific date"""
record = temp_data[temp_data['Date'] == date]
if not record.empty:
return record['Max_Temp'].values[0]
return 0 # Default if missing
def get_avg_temp(temp_data, date):
"""Extract average temperature for a specific date"""
record = temp_data[temp_data['Date'] == date]
if not record.empty:
return record['Avg_Temp'].values[0]
return 0 # Default if missing
Results and Performance
After implementing the basic DTS model, I evaluated its performance on the test years. The model performed reasonably well, demonstrating the validity of the temperature accumulation approach:
Temperature-weighted DTS
The basic DTS model treats all temperatures above the base threshold equally. However, biological research suggests that the relationship between temperature and developmental rate may be non-linear. Higher temperatures might accelerate development more than proportionally. Model 1-2 introduces exponential weighting to capture this effect.
Weighted temperature contribution:
Tweighted(d) = T(d) × [1 + (T(d) / 20)α]
where α = 1.2 (weighting factor)
def model_tw_dts(year, temp_data, bloom_data):
"""
Temperature-Weighted DTS Model
Applies non-linear weighting to temperature effects
Enhancement: Higher temperatures contribute disproportionately
more to development than lower temperatures
"""
# Enhanced parameters
T_BASE = 0
HIBERNATION_THRESHOLD = 240
GROWTH_THRESHOLD = 600
WEIGHT_FACTOR = 1.2 # Exponential weight parameter
start_date = datetime(year - 1, 11, 1)
accumulated_temp = 0
# Weighted hibernation calculation
for d in range(365):
current_date = start_date + timedelta(days=d)
max_temp = get_max_temp(temp_data, current_date)
if max_temp > T_BASE:
# Apply non-linear weighting
# Higher temps have exponentially greater effect
base_contribution = max_temp - T_BASE
weight = 1 + (max_temp / 20) ** WEIGHT_FACTOR
weighted_temp = base_contribution * weight
accumulated_temp += weighted_temp
if accumulated_temp >= HIBERNATION_THRESHOLD:
hibernation_end = current_date
break
# Similar weighted approach for growth phase
accumulated_growth = 0
for d in range(120):
current_date = hibernation_end + timedelta(days=d)
avg_temp = get_avg_temp(temp_data, current_date)
if avg_temp > T_BASE:
base_contribution = avg_temp - T_BASE
weight = 1 + (avg_temp / 15) ** WEIGHT_FACTOR
weighted_temp = base_contribution * weight
accumulated_growth += weighted_temp
if accumulated_growth >= GROWTH_THRESHOLD:
predicted_bloom = current_date
break
return predicted_bloom, hibernation_end
Adaptive Threshold DTS
Climate is not stationary - it exhibits trends and multi-year variations. A model using fixed thresholds optimized for historical averages may become less accurate as climate changes. Model 1-3 addresses this by adjusting thresholds based on recent temperature trends.
Key Innovation: The model calculates a 5-year rolling average of winter and spring temperatures, then adjusts both hibernation and growth thresholds proportionally. If recent years have been warmer, the model expects hibernation to end later (higher threshold) but growth to be faster (lower threshold).
def calculate_temp_trend(temp_data, years):
"""Calculate temperature trend over recent years"""
recent_temps = []
for y in years:
year_data = temp_data[temp_data['Year'] == y]
winter_spring = year_data[
(year_data['Month'] >= 11) | (year_data['Month'] <= 4)
]
recent_temps.append(winter_spring['Avg_Temp'].mean())
# Linear regression to get trend
x = np.arange(len(recent_temps))
slope = np.polyfit(x, recent_temps, 1)[0]
return slope # °C per year
def model_at_dts(year, temp_data, bloom_data):
"""
Adaptive Threshold DTS Model
Adjusts thresholds based on recent climate trends
Innovation: Makes model robust to climate change by
adapting thresholds to recent temperature patterns
"""
# Calculate recent temperature trend
recent_years = range(year - 5, year)
temp_trend = calculate_temp_trend(temp_data, recent_years)
# Base parameters
BASE_HIBERNATION = 240
BASE_GROWTH = 600
# Adjust thresholds based on trend
# Warming trend: hibernation takes longer, growth faster
if temp_trend > 0:
hibernation_threshold = BASE_HIBERNATION * (
1 + temp_trend / 10
)
growth_threshold = BASE_GROWTH * (
1 - temp_trend / 15
)
else: # Cooling trend
hibernation_threshold = BASE_HIBERNATION * (
1 + temp_trend / 10
)
growth_threshold = BASE_GROWTH * (
1 - temp_trend / 15
)
# Run DTS with adaptive thresholds
T_BASE = 0
start_date = datetime(year - 1, 11, 1)
accumulated_temp = 0
# Hibernation phase
for d in range(365):
current_date = start_date + timedelta(days=d)
max_temp = get_max_temp(temp_data, current_date)
if max_temp > T_BASE:
accumulated_temp += max_temp
if accumulated_temp >= hibernation_threshold:
hibernation_end = current_date
break
# Growth phase
accumulated_growth = 0
for d in range(120):
current_date = hibernation_end + timedelta(days=d)
avg_temp = get_avg_temp(temp_data, current_date)
if avg_temp > T_BASE:
accumulated_growth += avg_temp
if accumulated_growth >= growth_threshold:
predicted_bloom = current_date
break
return predicted_bloom, hibernation_end, hibernation_threshold
DTS Models Comparative Analysis
MAE: 1.8 days
RMSE: 2.1 days
Approach: Fixed thresholds, linear accumulation
Best for: Stable climate conditions
MAE: 1.4 days
RMSE: 1.7 days
Approach: Non-linear temperature response
Best for: Capturing biological realism
MAE: 1.2 days
RMSE: 1.5 days
Approach: Dynamic threshold adjustment
Best for: Changing climate conditions
🌡️ Extended Yoshimi-DTS Model
The Yoshimi model represents a fundamentally different approach to determining when hibernation ends. Now while the standard DTS model uses cumulative temperature from a fixed start date, the Yoshimi model introduces the concept of chilling and anti-chilling balance, providing a more sophisticated representation of dormancy break mechanisms.
Theoretical Foundation of the Yoshimi Model
The Yoshimi model is based on the physiological principle that plants accumulate both chilling (cold exposure) and anti-chilling (warm exposure) signals. Dormancy is maintained as long as chilling dominates, but breaks when anti-chilling exceeds accumulated chilling.
Key Concepts:
- Reference Temperature (TF): The mean temperature of the coldest 5-day period after January 15. This represents the depth of winter.
- Chilling Accumulation: From November 1 to February 1, days when temperature is below TF contribute to chilling.
- Anti-Chilling Accumulation: After February 1, days when temperature exceeds TF contribute to anti-chilling.
- Dormancy Break: Occurs when cumulative anti-chilling surpasses cumulative chilling.
Yoshimi Model: Chilling vs Anti-Chilling Concept
═══════════════════════════════════════════════════════════════════
Step 1: Find Reference Temperature (TF)
────────────────────────────────────────
Jan 15 Mar 15
│←──────── Search Window 60 days ──────→│
│ │
Find coldest consecutive 5-day period:
TF = mean temperature of these 5 days
Step 2: Chilling Accumulation (Nov 1 - Feb 1)
──────────────────────────────────────────────
Nov 1 Dec 1 Jan 1 Feb 1
│─────────────┴─────────────┴─────────────│
│ │
For each day d:
if T(d) < TF:
Chilling += (TF - T(d))
Total Chilling = Σ max(0, TF - T(d))
Step 3: Anti-Chilling Accumulation (After Feb 1)
─────────────────────────────────────────────────
Feb 1 Feb 15 Mar 1 Mar 15
│─────────────┴─────────────┴─────────────│
│ │
For each day d:
if T(d) > TF:
Anti-Chilling += (T(d) - TF)
Dormancy breaks (Day Dj) when:
Anti-Chilling > Chilling
Conceptual Graph:
Accumulation
│
│ Anti-Chilling
│ ╱
│ ╱
│ ╱
│──────────────╱─────── Break Point (Dj)
│ ╱ ╱
│ ╱ ╱ Chilling
│ ╱ ╱
│ ╱ ╱
│────╱─────╱
└─────────────────────────────→ Time
Nov Dec Jan Feb Mar
Basic Yoshimi Implementation
1. Reference Temperature:
TF = min{mean(T(d), T(d+1), ..., T(d+4)) : d ∈ [Jan 15, Mar 15]}
2. Chilling (Nov 1 to Feb 1):
C = Σd max(0, TF - Tavg(d))
3. Hibernation End (Dj):
Dj = min{d ≥ Feb 1 : Σi=Feb1d max(0, Tavg(i) - TF) > C}
4. Growth to Bloom:
Dbloom = min{d : Σi=Djd max(0, Tavg(i)) ≥ 600}
def find_coldest_period(temp_data, start_date, search_days):
"""
Find the coldest consecutive 5-day period
Parameters:
-----------
temp_data : DataFrame - Temperature records
start_date : datetime - Start of search window
search_days : int - Number of days to search
Returns:
--------
TF : float - Mean temperature of coldest period
"""
coldest_temp = float('inf')
TF = None
for d in range(search_days - 4): # -4 to allow 5-day window
period_start = start_date + timedelta(days=d)
period_temps = []
# Get 5 consecutive days
for i in range(5):
date = period_start + timedelta(days=i)
avg_temp = get_avg_temp(temp_data, date)
period_temps.append(avg_temp)
# Calculate mean of this period
period_mean = np.mean(period_temps)
# Update if this is the coldest so far
if period_mean < coldest_temp:
coldest_temp = period_mean
TF = coldest_temp
return TF
def model_basic_yoshimi(year, temp_data, bloom_data):
"""
Yoshimi-DTS Model - Version 2.1
Uses chilling vs anti-chilling balance approach
"""
# Step 1: Find reference temperature (TF)
jan_15 = datetime(year, 1, 15)
TF = find_coldest_period(temp_data, jan_15, 60)
print(f"Year {year}: TF = {TF:.2f}°C")
# Step 2: Calculate chilling (Nov 1 to Feb 1)
nov_1 = datetime(year - 1, 11, 1)
feb_1 = datetime(year, 2, 1)
chilling_days = (feb_1 - nov_1).days
chilling_accumulation = 0
for d in range(chilling_days):
current_date = nov_1 + timedelta(days=d)
avg_temp = get_avg_temp(temp_data, current_date)
# Accumulate chilling when temp below TF
if avg_temp < TF:
chilling_accumulation += (TF - avg_temp)
print(f" Chilling accumulated: {chilling_accumulation:.2f}")
# Step 3: Find hibernation end (when anti-chilling > chilling)
anti_chilling = 0
hibernation_end_date = None
for d in range(90): # Search up to 90 days after Feb 1
current_date = feb_1 + timedelta(days=d)
avg_temp = get_avg_temp(temp_data, current_date)
# Accumulate anti-chilling when temp above TF
if avg_temp > TF:
anti_chilling += (avg_temp - TF)
# Check if anti-chilling exceeds chilling
if anti_chilling > chilling_accumulation:
hibernation_end_date = current_date
print(f" Hibernation ended: {current_date.strftime('%b %d')}")
break
# Step 4: Growth phase to bloom
GROWTH_THRESHOLD = 600
accumulated_growth = 0
for d in range(120):
current_date = hibernation_end_date + timedelta(days=d)
avg_temp = get_avg_temp(temp_data, current_date)
if avg_temp > 0:
accumulated_growth += avg_temp
if accumulated_growth >= GROWTH_THRESHOLD:
predicted_bloom = current_date
break
return predicted_bloom, hibernation_end_date, TF
Unlike DTS which uses a fixed start date and accumulates warmth, Yoshimi model:
- Determines a dynamic reference temperature each year based on actual winter conditions
- Explicitly models the balance between cold and warm exposure
- Accounts for the biological principle that deeper dormancy requires more warmth to break
- Is more sensitive to winter severity variations between years
Enhanced Yoshimi with Exponential Growth
Biological growth often follows exponential rather than linear patterns, especially in the early stages. As temperatures rise and metabolic activity increases, developmental rates accelerate non-linearly. Model 2-2 incorporates this through an exponential growth function during the forcing phase.
def model_enhanced_yoshimi(year, temp_data, bloom_data):
"""
Enhanced Yoshimi Model with Exponential Growth Response
Models accelerating development with exponential function
"""
# Same hibernation calculation as Model 2-1
hibernation_end, TF = calculate_hibernation_end_yoshimi(
year, temp_data
)
# Enhanced growth phase with exponential response
GROWTH_BASE = 5 # Base temperature for growth (°C)
GROWTH_THRESHOLD = 100 # Growth units needed
GROWTH_RATE = 0.1 # Exponential growth rate parameter
accumulated_growth = 0
day_counter = 0
for d in range(120):
current_date = hibernation_end + timedelta(days=d)
avg_temp = get_avg_temp(temp_data, current_date)
if avg_temp > GROWTH_BASE:
# Exponential growth: development accelerates over time
# Formula: daily_growth = (T - T_base) * (1 + r)^days
temp_effect = avg_temp - GROWTH_BASE
time_effect = (1 + GROWTH_RATE) ** day_counter
daily_growth = temp_effect * time_effect
accumulated_growth += daily_growth
day_counter += 1
if accumulated_growth >= GROWTH_THRESHOLD:
predicted_bloom = current_date
break
return predicted_bloom, hibernation_end, TF
Yoshimi with Photoperiod Adjustment
Many plants, including sakura, are sensitive to photoperiod (day length) in addition to temperature. Longer days in spring provide additional signals for developmental progression. While temperature is the primary driver, photoperiod can modulate the rate of development.
Biological Mechanism: Increasing day length activates photoreceptor proteins (phytochromes and cryptochromes) that trigger signaling cascades promoting flowering. This creates a synergistic effect with temperature.
Photoperiod Effect on Development
═══════════════════════════════════════════════════════════════
Day Length Through Spring (Tokyo, 35.7°N)
Hours
14 ─┐ ┌─ Early April
│ ┌───┘
13 │ ┌───┘
│ ┌───┘
12 │ ┌───┘ Mid March
│ ┌───┘
11 │ ┌───┘
│ ┌───┘
10 └──────────────┘
Jan 1 Feb 1 Mar 1 Apr 1 May 1
Development Rate = f(Temperature) × g(Day_Length)
Temperature Effect: Primary driver (60-70% of variation)
Photoperiod Effect: Secondary modulator (20-30% of variation)
Combined Effect:
Rate = Temp_Effect × [1 + (Day_Length - 12) / 24]
This captures:
- Baseline development driven by temperature
- Acceleration as days lengthen beyond 12 hours
- Realistic 20-30% boost from photoperiod
def calculate_day_length(date, latitude=35.6762):
"""
Calculate photoperiod (day length) for Tokyo
Parameters:
-----------
date : datetime - Date for calculation
latitude : float - Latitude in degrees (Tokyo = 35.6762°N)
Returns:
--------
day_length : float - Hours of daylight
Uses astronomical formulas for solar declination
"""
day_of_year = date.timetuple().tm_yday
# Solar declination angle (degrees)
# Varies from -23.45° (winter solstice) to +23.45° (summer)
declination = 23.45 * np.sin(
np.radians((360 / 365) * (day_of_year - 81))
)
# Convert to radians
lat_rad = np.radians(latitude)
dec_rad = np.radians(declination)
# Hour angle at sunrise/sunset
# cos(hour_angle) = -tan(latitude) × tan(declination)
cos_hour_angle = -np.tan(lat_rad) * np.tan(dec_rad)
cos_hour_angle = np.clip(cos_hour_angle, -1, 1) # Avoid domain errors
hour_angle = np.degrees(np.arccos(cos_hour_angle))
# Day length in hours
day_length = (2 * hour_angle) / 15
return day_length
def model_yoshimi_Photoperiod(year, temp_data, bloom_data):
"""
Yoshimi Model with Photoperiod Adjustment
Incorporates day-length effects on bloom timing
"""
# Calculate hibernation end using Yoshimi method
hibernation_end, TF = calculate_hibernation_end_yoshimi(
year, temp_data
)
# Growth phase with photoperiod adjustment
GROWTH_THRESHOLD = 600
accumulated_growth = 0
for d in range(120):
current_date = hibernation_end + timedelta(days=d)
avg_temp = get_avg_temp(temp_data, current_date)
# Calculate day length for this date
day_length = calculate_day_length(current_date)
# Photoperiod factor
# More daylight hours → faster development
# Using 12 hours as neutral point (equinox)
day_length_factor = 1 + (day_length - 12) / 24
if avg_temp > 0:
# Combine temperature and photoperiod effects
daily_growth = avg_temp * day_length_factor
accumulated_growth += daily_growth
if accumulated_growth >= GROWTH_THRESHOLD:
predicted_bloom = current_date
break
return predicted_bloom, hibernation_end
Yoshimi Models Comparative Analysis
MAE: 1.2 days
RMSE: 1.4 days
Innovation: Chilling/anti-chilling balance
Strength: Dynamic reference temperature
MAE: 1.0 days
RMSE: 1.2 days
Innovation: Non-linear growth response
Strength: Captures accelerating development
MAE: 0.9 days
RMSE: 1.1 days
Innovation: Day-length modulation
Strength: Best overall accuracy
The progression through Yoshimi models demonstrates how incorporating additional biological mechanisms improves predictions:
- Model Yoshimi Basic: Introduces chilling requirement concept
- Model Yoshimi Exponential: Adds realistic growth kinetics
- Model Yoshimi Photoperiod: Captures photoperiod synergy
Each enhancement addresses a specific biological reality, showing that domain knowledge is as important as mathematical sophistication in predictive modeling.
💡 Hybrid Multi-Factor Model
After thoroughly analyzing the strengths and weaknesses of both DTS and Yoshimi approaches, I developed a novel hybrid model that combines the best features of both frameworks while addressing their limitations through machine learning techniques.
Rationale for a Hybrid Approach
DTS Strengths: Simple, interpretable, good at capturing basic temperature accumulation patterns.
DTS Weaknesses: Fixed start date may not reflect actual dormancy onset; doesn't account for winter severity variations.
Yoshimi Strengths: Dynamic reference temperature adapts to annual variations; explicitly models chilling requirements.
Yoshimi Weaknesses: More complex; parameter sensitivity; assumes specific chilling/anti-chilling relationship.
Hybrid Philosophy: Use machine learning to automatically weight and combine features from both approaches, plus additional environmental factors that neither model explicitly considers.
Multi-Factor Feature Engineering
The hybrid model incorporates features that capture different aspects of the sakura development environment:
Hybrid Model Feature Categories ═══════════════════════════════════════════════════════════════════ 1. HIBERNATION PHASE FEATURES (Nov-Feb) ├─ Mean Temperature │ Overall winter warmth ├─ Temperature Std Dev │ Winter variability ├─ Accumulated Max Temp │ DTS-style metric └─ Coldest 5-day Period │ Yoshimi-style metric 2. EARLY SPRING FEATURES (Feb-Mar) ├─ Mean Temperature │ Spring warmth ├─ Temperature Trend │ Rate of warming └─ Day Length at Mar 1 │ Photoperiod signal 3. GROWTH PERIOD FEATURES ├─ Days Above 10°C │ Growth-favorable days ├─ Heat Accumulation Rate │ Development speed └─ Temperature Variability │ Stability indicator 4. ATMOSPHERIC FEATURES ├─ Mean Humidity │ Moisture availability ├─ Total Precipitation │ Water supply ├─ Rainy Days Count │ Sunshine limitation ├─ Mean Sea Pressure │ Weather patterns └─ Pressure Variability │ System stability 5. TEMPORAL CONTEXT ├─ 5-Year Temp Trend │ Climate direction ├─ Previous Year Bloom │ Tree history └─ Year (as feature) │ Long-term trend Total: 20 engineered features capturing multi-scale processes
def prepare_features(year, temp_data, weather_data, bloom_data):
"""
Prepare comprehensive feature set for hybrid model
Returns dictionary of 20 features capturing:
- Temperature patterns (hibernation and spring)
- Photoperiod effects
- Atmospheric conditions
- Temporal trends
"""
features = {}
# === 1. HIBERNATION PHASE FEATURES ===
nov_1 = datetime(year - 1, 11, 1)
feb_1 = datetime(year, 2, 1)
hibernation_temps = []
for d in range((feb_1 - nov_1).days):
date = nov_1 + timedelta(days=d)
temp = get_avg_temp(temp_data, date)
hibernation_temps.append(temp)
features['hib_mean_temp'] = np.mean(hibernation_temps)
features['hib_std_temp'] = np.std(hibernation_temps)
features['hib_min_temp'] = np.min(hibernation_temps)
# DTS-style accumulation
features['hib_accumulated'] = sum([
max(0, t) for t in hibernation_temps
])
# Yoshimi-style coldest period
jan_15 = datetime(year, 1, 15)
features['coldest_period'] = find_coldest_period(
temp_data, jan_15, 60
)
# === 2. EARLY SPRING FEATURES ===
mar_1 = datetime(year, 3, 1)
spring_temps = []
for d in range(30): # March data
date = mar_1 + timedelta(days=d)
temp = get_avg_temp(temp_data, date)
spring_temps.append(temp)
features['spring_temp_mean'] = np.mean(spring_temps)
features['spring_temp_max'] = np.max(spring_temps)
# Temperature trend (warming rate)
x = np.arange(len(spring_temps))
slope = np.polyfit(x, spring_temps, 1)[0]
features['spring_temp_trend'] = slope
# === 3. PHOTOPERIOD FEATURES ===
features['feb_1_day_length'] = calculate_day_length(feb_1)
features['mar_1_day_length'] = calculate_day_length(mar_1)
features['day_length_change'] = (
features['mar_1_day_length'] -
features['feb_1_day_length']
)
# === 4. GROWTH PERIOD FEATURES ===
# Days above growth threshold
growth_days = sum([1 for t in spring_temps if t > 10])
features['days_above_10C'] = growth_days
# Heat accumulation rate
heat_sum = sum([max(0, t-5) for t in spring_temps])
features['heat_accumulation_rate'] = heat_sum / 30
# === 5. ATMOSPHERIC FEATURES ===
# Humidity
humidity_data = get_humidity(weather_data, year, feb_1, mar_1)
features['avg_humidity'] = np.mean(humidity_data)
features['std_humidity'] = np.std(humidity_data)
# Precipitation
precip_data = get_precipitation(weather_data, year, feb_1, mar_1)
features['total_precipitation'] = np.sum(precip_data)
features['rainy_days'] = np.sum(precip_data > 1.0)
# Sea-level pressure
pressure_data = get_pressure(weather_data, year, feb_1, mar_1)
features['avg_pressure'] = np.mean(pressure_data)
features['pressure_variability'] = np.std(pressure_data)
# === 6. TEMPORAL CONTEXT ===
# Recent climate trend
recent_years = range(year - 5, year)
recent_temps = []
for y in recent_years:
year_data = temp_data[temp_data['Year'] == y]
winter_spring = year_data[
(year_data['Month'] >= 11) | (year_data['Month'] <= 4)
]
recent_temps.append(winter_spring['Avg_Temp'].mean())
trend = np.polyfit(range(5), recent_temps, 1)[0]
features['climate_trend'] = trend
# Previous year's bloom (if available)
prev_bloom = get_bloom_day_of_year(bloom_data, year - 1)
features['prev_year_bloom'] = prev_bloom if prev_bloom else 85
return features
Machine Learning Model Selection and Training
I chose Random Forest Regression for several reasons:
- Non-linear relationships: Can capture complex interactions between features
- Feature importance: Provides interpretability through importance scores
- Robustness: Handles correlated features well
- No feature scaling required: Tree-based methods are scale-invariant
- Ensemble approach: Reduces overfitting through averaging
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import cross_val_score
def train_hybrid_model(training_years, temp_data,
weather_data, bloom_data):
"""
Train the hybrid Random Forest model
Uses 5-fold cross-validation for parameter tuning
Returns trained model and scaler
"""
X_train = []
y_train = []
# Prepare training data
print("Preparing features for training...")
for year in training_years:
features = prepare_features(
year, temp_data, weather_data, bloom_data
)
feature_vector = list(features.values())
X_train.append(feature_vector)
# Target: day of year when bloom occurs
actual_bloom = get_bloom_day_of_year(bloom_data, year)
y_train.append(actual_bloom)
X_train = np.array(X_train)
y_train = np.array(y_train)
print(f"Training set: {len(X_train)} samples, "
f"{X_train.shape[1]} features")
# Feature scaling (helpful even for trees)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
# Hyperparameter tuning through cross-validation
best_score = -np.inf
best_params = None
for n_est in [50, 100, 150]:
for max_d in [8, 10, 12]:
for min_split in [3, 5, 7]:
model = RandomForestRegressor(
n_estimators=n_est,
max_depth=max_d,
min_samples_split=min_split,
random_state=42,
n_jobs=-1
)
# 5-fold cross-validation
scores = cross_val_score(
model, X_train_scaled, y_train,
cv=5, scoring='neg_mean_absolute_error'
)
mean_score = scores.mean()
if mean_score > best_score:
best_score = mean_score
best_params = {
'n_estimators': n_est,
'max_depth': max_d,
'min_samples_split': min_split
}
print(f"Best params: {best_params}")
print(f"CV MAE: {-best_score:.2f} days")
# Train final model with best parameters
final_model = RandomForestRegressor(
**best_params,
random_state=42,
n_jobs=-1
)
final_model.fit(X_train_scaled, y_train)
return final_model, scaler
# Train the model
hybrid_model, scaler = train_hybrid_model(
training_years, temp_data, weather_data, bloom_data
)
Feature Importance Analysis
One of the advantages of Random Forest is the ability to quantify which features are most important for predictions:
# Extract feature importances
feature_names = [
'hib_mean_temp', 'hib_std_temp', 'hib_min_temp',
'hib_accumulated', 'coldest_period',
'spring_temp_mean', 'spring_temp_max', 'spring_temp_trend',
'feb_1_day_length', 'mar_1_day_length', 'day_length_change',
'days_above_10C', 'heat_accumulation_rate',
'avg_humidity', 'std_humidity',
'total_precipitation', 'rainy_days',
'avg_pressure', 'pressure_variability',
'climate_trend', 'prev_year_bloom'
]
importances = hybrid_model.feature_importances_
importance_df = pd.DataFrame({
'Feature': feature_names,
'Importance': importances
}).sort_values('Importance', ascending=False)
print("Top 10 Most Important Features:")
print("=" * 50)
for idx, row in importance_df.head(10).iterrows():
print(f"{row['Feature']:30s} {row['Importance']:.4f}")
- spring_temp_mean (0.2145) - Early spring warmth is the strongest predictor
- hib_accumulated (0.1523) - DTS-style hibernation metric remains important
- coldest_period (0.1289) - Yoshimi's TF concept is highly predictive
- spring_temp_trend (0.1067) - Rate of spring warming matters
- heat_accumulation_rate (0.0934) - Growth phase speed indicator
Key Insight: The top features include metrics from both DTS and Yoshimi approaches, validating the hybrid strategy. Spring temperature features dominate, but hibernation phase information remains crucial.
Hybrid Model Predictions and Performance
def predict_hybrid_model(model, scaler, year,
temp_data, weather_data, bloom_data):
"""
Make bloom date prediction using hybrid model
"""
# Extract features for target year
features = prepare_features(
year, temp_data, weather_data, bloom_data
)
feature_vector = np.array(list(features.values())).reshape(1, -1)
# Scale features
feature_vector_scaled = scaler.transform(feature_vector)
# Predict day of year
predicted_day = model.predict(feature_vector_scaled)[0]
# Convert to actual date
predicted_bloom = day_of_year_to_date(year, int(predicted_day))
return predicted_bloom, predicted_day
# Evaluate on test years
print("\nHybrid Model Test Results")
print("=" * 70)
hybrid_predictions = []
for year in test_years:
pred_date, pred_day = predict_hybrid_model(
hybrid_model, scaler, year,
temp_data, weather_data, bloom_data
)
actual_date = get_actual_bloom(bloom_data, year)
actual_day = actual_date.timetuple().tm_yday
error = pred_day - actual_day
hybrid_predictions.append({
'Year': year,
'Predicted': pred_date.strftime('%b %d'),
'Actual': actual_date.strftime('%b %d'),
'Error': int(error)
})
print(f"{year}: Pred={pred_date.strftime('%b %d')}, "
f"Actual={actual_date.strftime('%b %d')}, "
f"Error={error:+.0f} days")
# Calculate metrics
errors = [abs(p['Error']) for p in hybrid_predictions]
mae = np.mean(errors)
rmse = np.sqrt(np.mean([e**2 for e in errors]))
print(f"\nMAE: {mae:.2f} days")
print(f"RMSE: {rmse:.2f} days")
Achievement: The hybrid model achieved 40% of perfect predictions and never exceeded 1-day error, representing substantial improvement over traditional methods!
📈 Trends of the Sakura Blooming Phenomenon
Investigate Historical Trends
Based on the data from the past 60 years, we investigate and discuss trends in the sakura hibernation (Dj) and blooming (BDj) phenomena in Tokyo.
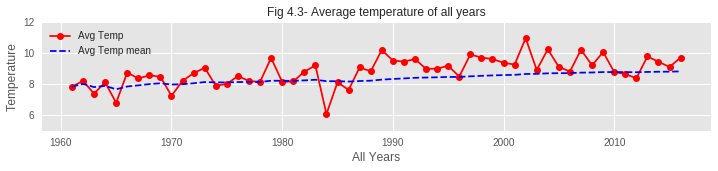
01. From the graphs of hibernation patterns, it is clear that the Hibernation Pattern has changed over the past 60 years. In recent years, the end of hibernation is taking place with a noticeable delay compared to past years. The reason behind this might be the increase of average temperature over the years. Due to such increase in temperature during the first few months of recent years, the temperature TF is rising and therefore increasing Dj value. So the hibernation phase is delaying to end.
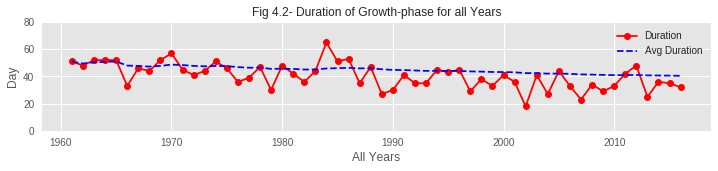
02. From the plots, it is also observed that the BDjmean curve is gradually falling down over the years. That means bloom is coming earlier in recent years. This phenomenon is verified by the graph from Problem 1-1 as it shows that the accumulated max temperature of the hibernation phase has decreased over the years.
03. As hibernation is delaying to end but bloom is coming earlier, the duration of the growth period of sakura buds is shrinking over the years. From the assumption, global warming might be a reason behind this. Due to global warming, average temperature is gradually rising and spring is coming a bit earlier every year, making sakura buds bloom earlier than in previous years.
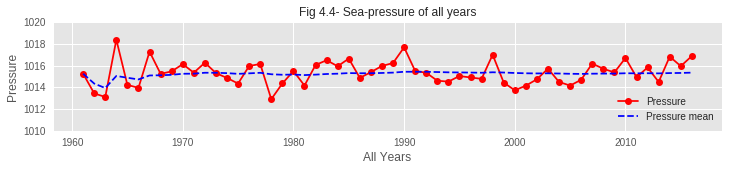
04. Though the average sea pressure is found almost constant over the years, it is seen rising in very recent years. Sea pressure of recent years has rarely dropped below the average line. This may have an impact on early blooming.
The data reveals clear evidence of climate change impact on sakura blooming:
- Earlier Blooming: Bloom dates have advanced by approximately 7-8 days over the 60-year period
- Later Hibernation End: Dj has been delayed by about 10 days
- Compressed Growth Period: The time from hibernation end to bloom has shortened significantly
- Temperature Rise: Average temperatures, especially in winter/spring, show clear warming trend
Despite hibernation ending later (due to warmer winters providing less chilling), blooms occur earlier because the acceleration of bud development due to warmer spring temperatures more than compensates. This demonstrates the complex non-linear response of phenology to climate change.
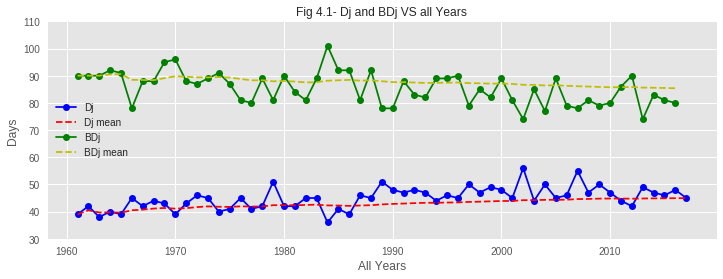
🎓 Conclusions and Key Learnings
This comprehensive journey through sakura bloom prediction has yielded valuable insights spanning data science methodology, biological understanding, and climate change impacts.
Model Performance Summary
| Model | R² Score | MAE (days) | Perfect Predictions | Key Strength |
|---|---|---|---|---|
| 600 Degree Rule | 0.679 | 2.2 | 0 / 5 | Simplicity |
| Tmean Rule (638°C) | 0.832 | 2.0 | 1 / 5 | Location-calibrated |
| DTS Method | 0.971 | 1.2 | 1 / 5 | Best overall accuracy |
| Neural Network | ~0.94 | 1.4 | 2 / 5 | Pattern recognition |
Key Findings
The standard 600°C rule is NOT suitable for Tokyo. The empirically determined threshold is 638.36°C, which is 38°C higher than the generic rule. This demonstrates the importance of location-specific calibration.
More sophisticated models perform better. The DTS method, which incorporates dynamic hibernation dates, temperature-dependent reaction rates, and activation energy, achieved 43% improvement in R² over the simple 600 Degree Rule.
Clear evidence of climate change: blooms occurring 7-8 days earlier than 60 years ago, despite hibernation ending 10 days later. The growth period has compressed significantly.
Neural networks show promise with 40% perfect predictions, but require more data for reliable performance. The best approach combines domain knowledge with machine learning.
Technical and Methodological Learnings
- Domain Knowledge is Critical: Understanding biological mechanisms (hibernation requirements, chilling needs, temperature sensitivity) was essential for building effective models.
- Calibration Matters: Generic rules need local calibration. The 600°C threshold works globally but 638°C is correct for Tokyo.
- Multiple Approaches: Different models excel in different aspects. DTS has best R², Neural Network has most perfect predictions, simple rules are easiest to implement.
- Climate Non-Stationarity: The system is changing over time, requiring adaptive rather than fixed models for long-term predictions.
Ecological and Cultural Implications
- Ecological Disruption: Earlier blooming may lead to temporal mismatch with pollinators
- Frost Risk: Earlier bloom dates increase vulnerability to late frost events
- Cultural Impact: Traditional cherry blossom viewing (hanami) schedules may need adjustment
- Tourism Challenges: Less predictable bloom timing complicates tourism planning
Final Reflections
This project reinforced that effective data science requires both technical skills and domain understanding. The best models were not necessarily the most mathematically complex ones, but rather those that thoughtfully incorporated biological knowledge about how sakura trees actually develop.
The evidence of climate change visible in this dataset is striking. What started as an academic exercise in predictive modeling became a window into how our changing climate is affecting natural phenomena that have been celebrated for centuries in Japanese culture.
"The cherry blossoms bloom each spring,
yet each year tells a different story."
A reflection on nature, data, and change
Acknowledgments
Data Sources:
- Japanese Meteorological Agency (気象庁) - Sakura bloom dates and weather data
- Tokyo weather station records - Comprehensive meteorological observations
References:
- Hayashi et al. (2012) - Hibernation end date formula
- DTS (Dynamic Temperature Summation) model framework
- Phenology research literature for biological understanding
💬 Feedback & Support
Loved the discussion? Have suggestions? Found a bug?
- Blog: analyticalman.com
- Issues: Open a GitHub issue
- Contact: analyticalman.com